آنچه در تحلیل نتایج مقاومت بتن برای مهندسین، دانشمندان و متخصصین فنی ضروری است، آشنایی با علوم مختلفی چون ریاضیات و تحلیل آماری است؛ زیرا با استفاده از این علوم میتوان دادههای آماری به دست آمده از نتایج مقاومت بتن را ارزیابی نمود. سؤال اینجاست که چرا باید نتایج و دادههای تحلیل مقاومت بتن را ارزیابی کرد؟ و چه اصطلاحاتی برای ارزیابی دادههای آماری مقاومت بتن به کار میرود؟ در این مقاله از بلاگ رامکا به معرفی اصطلاحات رایج در تحلیل و ارزیابی نتایج مقاومت بتن و میزان اهمیت تحلیل مقاومت بتن خواهیم پرداخت. پس در ادامه با ما همراه باشید.
اصطلاحات تحلیل نتایج مقاومت بتن
بتن مخلوطی از آب، سنگدانه و سیمان است که برای بررسی میزان مقاومت آن، لازم است نتایج حاصل از مقاومت بتن مورد ارزیابی قرار گیرد. به طور معمول، بسیاری از مهندسین و متخصصین فنی با اصطلاحات و علایم مورد استفاده در تحلیل نتایج مقاومت بتن آشنایی دارند، اما ممکن است برخی با این علایم و اصطلاحات آشنا نباشند. از این رو در ذیل، مجموعهای از اصطلاحات به همراه علایم متداول آن ارائه خواهد شد.
X̅: مقاومت متوسط – میانگین عددی مقاومت کلیه نمونههای مورد نظر
σ: انحراف معیار- جذر میانگین مربعات انحراف هر مقاومت از مقاومت متوسط. انحراف معیار به کمک جذر گرفتن از میانگین مربعات انحراف هر یک از مقاومتها از مقاومت متوسط به دست میآید، لذا
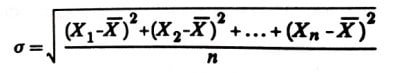
n: مجموع تعداد آزمایشها
V: ضریب پراکندگی- انحراف معیار که بر حسب درصدی از مقاومت متوسط بیان میشود:
V=(σ/X̅)۱۰۰
R: دامنۀ مقاومتها- اختلاف عددی میان بالاترین و پایینترین مقاومت آزمایشهای مورد بررسی
f’c : مقاومت مشخصه
fcr: مقاومت متوسط لازم- مقاومت متوسطی که مورد نیاز است و با روشهای آماری تعیین میشود تا تعداد نمونههایی که نتیجه آنها پایینتر از مقاومت مشخصه (f’c) است، بیش از یک مقدار مشخص نشود.
fcr=f’c /(1-tV)
که در این رابطه:
t: عدد ثابت که به درصد نمونههای مجاز پایینتر از f’c وتعداد آزمایشهایی که جهت تعیین V مورد بررسی قرار گرفتهاند، وابسته است.
| احتمال مقاومت در محدوده X̅±tσ (درصد) | احتمال مقاومت کمتر از X̅±tσ | t |
| 40 | 3 در ۱۰ | ۰٫۵۲ |
| ۵۰ | ۲٫۵ در ۱۰̅ | ۰٫۶۷ |
| ۶۰ | ۲ در ۱۰ | ۰٫۸۴ |
| ۶۸٫۲۷ | ۱ در ۶٫۳ | ۱٫۰۰ |
| ۷۰ | ۱٫۵ در ۱۰ | ۱٫۰۴ |
| ۸۰ | ۱ در ۱۰ | ۱٫۲۸ |
| ۹۰ | ۱ در ۲۰ | ۱٫۶۵ |
| ۹۵ | ۱ در ۴۰ | ۱٫۹۶ |
| ۹۵٫۴۵ | ۱ در ۴۴ | ۲٫۰۰ |
| ۹۸ | ۱ در ۱۰۰ | ۲٫۳۳ |
| ۹۹ | ۱ در ۲۰۰ | ۲٫۵۸ |
| ۹۹٫۷۳ | ۱ در ۷۴۱ | ۳٫۰۰ |
σ۱: انحراف معیار هر آزمایش- انحراف معیار نمونهها در آزمایشی معین که ترجیحاً بر اساس نتیجه حداقل ۱۰ سری نمونه محاسبه میشود.
σ۱=۱/d2(R̅)
که در این رابطه: ۱ بر d2= عدد ثابتی است که به تعداد نمونهها بستگی دارد.
| تعداد نمونهها | d2 | 1 بر d2 |
| 2 | 1.128 | 0.8865 |
| 3 | 1.693 | 0.5907 |
| 4 | 2.059 | 0.4857 |
| 5 | 2.326 | 0.4299 |
| 6 | 2.534 | 0.3946 |
| 7 | 2.704 | 0.3698 |
| 8 | 2.847 | 0.3512 |
| 9 | 2.970 | 0.3367 |
| 10 | 3.078 | 0.3249 |
فرمول: دامنه متوسط – متوسط دامنۀ (R̅) سری نمونههایی که برای تعیین σ۱ مورد استفاده قرار گرفتند.
V1 : ضریب پراکندگی هر آزمایش – ضریب پراکندگی میان نتایج نمونههای استوانهای در هر مخلوط معین
V1=(X̅/σ۱)×۱۰۰
آزمایش: دستهای از نمونههای آزمایشی (به طور معمول دو یا سه) که همگی از یک نمونه ساخته شده و در سن یکسان آزمایش شدهاند.
بیشتر بخوانید: بتن پرمقاومت
ملزومات کنترل کیفیت بتن
کنترل کیفیت بتن در تحلیل نتایج مقاومت بتن، مستلزم کنترل طیف گستردهای از فعالیتها، نظیر مطابقت هر جزء تشکیل دهنده بتن با مشخصات استاندارد و همچنین، رعایت روش صحیح اختلاط، ریختن و عمل آوردن بتن است. معمولاً راندمان عملکرد در ساخت بتن، آزمایش کردن و کنترل اجزای تشکیل دهنده آن، عامل تعیینکننده درجۀ یکنواختی و کیفیت بتن است. استفاده از روشهای تحلیل آماری برای تعیین درجه یکنواختی و کیفیت بتن ضروری است.
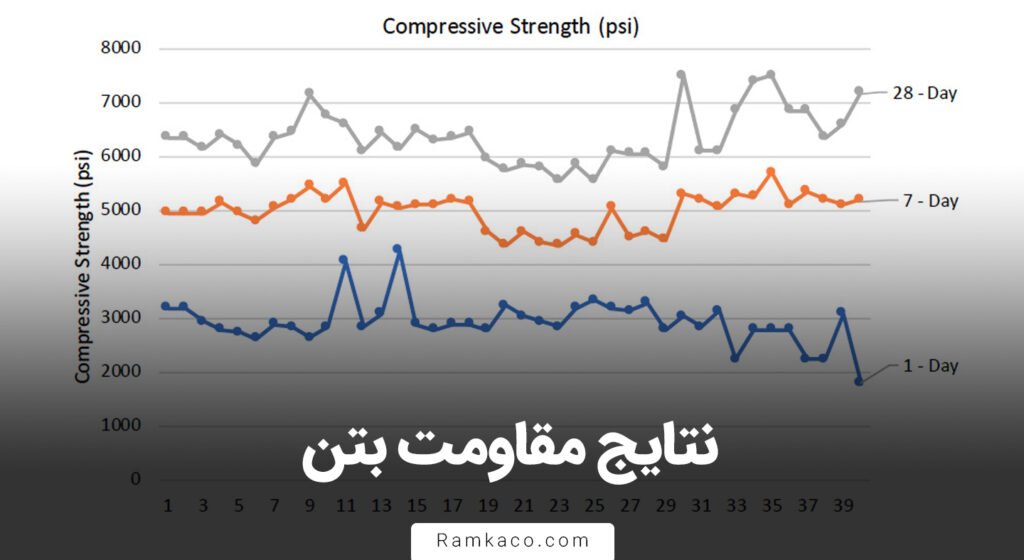
موسسه ACI، روشی جهت ارزیابی نتایج آزمایش مقاومت فشاری بتن کارگاهی که بدین منظور تهیه شده، پیشنهاد میکند. برای انجام این گونه مطالعات، بایستی آزمایش تعیین مقاومت فشاری بتن کارگاهی، به تعداد کافی و طبق استانداردهای قابل قبول صورت گیرد. نتایج آزمایش تعیین مقاومت بتن، درون منحنی نرمال فراوانی- توزیع قرار میگیرد که این مطلب در شکل زیر دیده میشود. اولین نتیجۀ این تحلیل، این واقعیت است که پراکندگی نتایج وجود دارد و تعیین یک حداقل مطلق مقاومت فشاری امکانپذیر نیست.
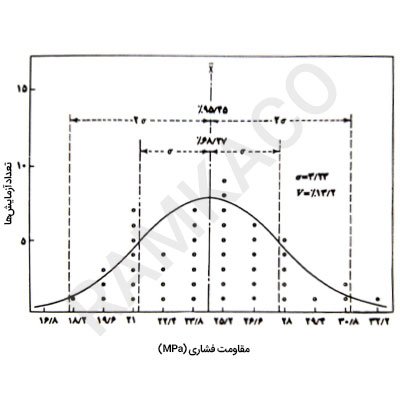
بر اساس قانون احتمالات دیده شده یک مقاومت در هر ۶ آزمایش، بیش از انحراف معیار (σ) زیر مقاومت متوسط، یک مقاومت در هر ۴۴ آزمایش، بیش از دو برابر انحراف معیار کمتر از مقاومت متوسط و یک مقاومت در هر ۷۴۱ آزمایش بیش از ۳ برابر انحراف معیار، کمتر از مقاومت متوسط خواهد بود.
ملزومات پذیرش مقاومت بتن، بر اساس آییننامه ACI
معیار آییننامه ساختمانیACI برای ارزیابی بتن این است که مقاومت متوسط بتن تولید شده، همیشه باید بیش از مقاومت مشخصه (f’c) که در مرحله طراحی سازه به کار رفته است باشد. مفهوم احتمال به کمک نتایج آزمایش که پایینتر از f’c هستند، میآید. این قانون تصریح میکند مقاومتِ هیچ آزمایشی بیش از ۳٫۵ مگاپاسکال، پایینتر از مقاومت مشخصه f’c نباشد.
آییننامه ساختمانی ACI تصریح میکند نمونهگیری آزمایش مقاومت هر رده بتن، باید حداقل یک بار در روز و هر ۱۱۰ متر مکعب بتن یا در هر ۴۵۰ متر مربع بتنریزی سطح انجام شود. نمونههای آزمایش مقاومت، باید طبق روش استاندارد نمونهگیری از بتن تازه (ASTM C172) گرفته شوند.
نمونههای استوانهای برای آزمایشهای پذیرش بتن، طبق روش استاندارد ساخت و عمل آوردن نمونههای آزمایش مقاومت فشاری و خمشی بتن در کارگاه (ASTM C31) قالبگیری شده و در آزمایشگاه عملآوری شوند و طبق روش آزمایش مقاومت فشاری، نمونههای استوانهای بتن (ASTM C39) آزمایش گردند. هر نتیجه آزمایش مقاومت، بایستی متوسط دو نمونه استوانهای از یک نمونه یکسال در سن ۲۸ روز یا سن معین کمتر باشد.
اگر نتایج آزمایش نمونههایی که در آزمایشگاه عملآوری شدهاند، بیش از ۳٫۵ مگاپاسکال از f’c باشد و محاسبات نشان دهد ظرفیت باربری به میزان زیادی تقلیل یافته است، مغزهگیری از محل مورد تردید و آزمایش آن، روش استاندارد به دست آوردن و آزمایش مغزههای گرفته شده و تیرهای بریده شده از بتن (ASTM 42) میتواند انجام شود. به ازای هر آزمایش نمونه استوانهای که بیش از ۳٫۵ مگاپاسکال کمتر از f’c باشد، باید ۳ مغزه گرفته شود.
بتن واقع در محلی که آزمایش روی مغزههای آن انجام میشود، هنگامی از لحاظ سازهای پذیرفته میشود که متوسط مقاومت سه مغزه حداقل برابر ۸۵% f’c باشد و مقاومت هیچ مغزهای به تنهایی کمتر از ۷۵% f’c نباشد. جهت اطمینان از دقت آزمایش، نقاطی که مغزههای گرفته شده از آن نتایج غیرمنطقی دهند را میتوان مجدداً آزمایش کرد. اگر این معیار پذیرش مقاومت برآورده نشود، میتوان دستور انجام آزمایشهای بارگذاری مطابق آییننامه ساختمانی ACI را صادر نمود.
منحنیهای کنترل کیفیت بتن
روشی مناسب و مطمئن برای تحلیل روند تغییر مقاومت بتن به صورت ترسیمی، استفاده از منحنیهای کنترل است. شکل زیر نمونهای از منحنیهای کنترل برای بتن سازهای است که در آن، نتیجه هر آزمایش مقاومت فشاری در سن ۲۸ روز دیده میشود. منحنی به این شکل نشان میدهد که چه تعداد نمونه استوانهای زیر مقاومت مشخصه است و اینکه آیا شرایط پذیرش بتن را برآورده میکند. ترسیم این منحنی به صورت روزانه به نحو مؤثری نشان میدهد آیا روند نامطلوب مقاومت رخ داده است.

در این صورت، باید با اقداماتی چون: تغییر طرح اختلاط، مصالح، و نحوۀ اختلاط و…، اقدام به تصحیح فوری کرد. مقاومت مشخصه (f’c) و مقاومت متوسط لازم (fcr)در این منحنی نشان داده شدهاند. fcr از رابطه زیر به دست میآید:
fcr=f’c/(1-tV)
که در این رابطه، t از جدول بالا به دست میآید و V ضریب پراکندگی است. منحنی دیگری که در این روش تحلیل مفید است، منحنی میانگین متحرک است که در شکل نشان داده شده است. میانگین متحرک مقاومت برای پنج سری نمونههای استوانهای قبلی رسم شده که طبق مشخصات حد پایین آن مقاومت مشخصه f’c است. میانگین متحرک دامنه برای ۱۰ گروه از نمونههای استوانهای قبلی رسم میشود. به جهت انجام کنترل کیفیت مناسب، پراکندگی هر آزمایش (V1) باید حداکثر ۵% باشد. لذا برای کنترل، حداکثر دامنه متوسط برابر است با:
(برای دو نمونه استوانهای در هر سری)
R̅m=(0.05×۱٫۱۲۸) f’c=0.0564 f’cr
(برای سه نمونه استوانهای در هر سری)
R̅m=(0.05×۱٫۶۹۳) f’c=0.08465 f’cr
ارزیابی آماری مقاومت بتن
اطلاعات آماری برای ارزیابی مقاومت فشاری هر رده یا نوع بتن به صورت مجزا به کار میرود. علاوه بر استفاده از روابط آماری برای ترسیم نمودارهای کنترل، روشهای آماری توصیه شده نیز برای محاسبه انحراف معیار و ضریب پراکندگی مورد استفاده قرار میگیرد. مراحل استفاده به شرح زیر است :
- X̅ مقاومت متوسط همه نمونههای آزمایش در سن ۲۸ روز (ترجیحاً بعد از اینکه نتیجه ۳۰ آزمایش موجود باشد) را به کمک رابطه زیر محاسبه کنید:
X̅=(X1+X2+X3+…+Xn)/n
که در این رابطه X1، X2، X3 و… و Xn مقاومت هر آزمایش و n تعداد کل آزمایشها است.
- انحراف معیار (σ) را به کمک رابطۀ زیر محاسبه کنید (منحنی فراوانی نرمال را به عنوان نمونه ترسیمی مشاهده فرمایید):
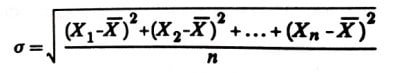
- ضریب پراکندگی (V) را به کمک رابطۀ زیر محاسبه کنید:
V= σ/X̅×۱۰۰
جدولی که در ادامه میآید، ضرایب پراکندگی مختلف را به صورت طبقهبندی شده ارائه میکند. همانطور که در شکل بعد از جدول زیر ملاحظه میکنید، هر چه این ضریب بیشتر باشد، مقاومت متوسط بتن نیز بایستی بالاتر باشد و لذا طرح اختلاط پُرهزینهتر میشود. این موضوع بر اهمیت انجام کنترل کیفیت مناسب تأکید میکند.
- علاوه بر ارزیابی آماری مقاومت بتن که در بالا بیان شد، لازم است یکنواختی نمونههای استوانهای نیز تعیین شود. این عامل همانطور که قبلاً گفته شد، راندمان ساخت، عمل آوردن و آزمایش بتن را نشان میدهد. انحراف معیار (σ۱) و ضریب پراکندگی (V1) هر آزمایش به طریق زیر محاسبه میشود:
σ۱=(۱/d2)R̅
V1=(σ۱/X̅)×۱۰۰
که در این روابط :
X̅: مقاومت متوسط
R̅: دامنۀ متوسط گروههای نمونههای استوانهای
۱ بر d2: عدد ثابت که به تعداد نمونههای استوانهای در هر گروه بستگی دارد و از جدول ۲ به دست میآید.
انحراف معیار برای استانداردهای مختلف کنترل کیفیت بتن (MPa)
| رده انجام کنترل کیفیت | عالی | خیلی خوب | خوب | متوسط | ضعیف |
پراکندگی کلی
| آزمایش در ساختمانهای متعارف | ۲٫۸˂ | ۳٫۵-۲٫۸ | ۴٫۲-۳٫۵ | ۴٫۹-۴٫۲ | ۴٫۹ ˃ |
| نمونههای آزمایشگاهی | ۱٫۴˂ | ۱٫۷۵-۱٫۴ | ۱٫۷۵-۲٫۱ | ۲٫۴۵-۲٫۱ | ۲٫۴۵ ˃ |
ضریب پراکندگی در استانداردهای مختلف کنترل کیفیت بتن (درصد)
| رده انجام کنترل کیفیت | عالی | خیلی خوب | خوب | متوسط | ضعیف |
پراکندگی هر آزمایش
| آزمایش کنترل کارگاهی | ۳٫۰˂ | ۴٫۰-۳٫۰ | ۵٫۰-۴٫۰ | ۶٫۰-۵٫۰ | ۶٫۰ ˃ |
| مخلوطهای آزمایشی آزمایشگاهی | ۲٫۰˂ | ۳٫۰-۲٫۰ | ۴٫۰-۳٫۰ | ۵٫۰-۴٫۰ | ۵٫۰ ˃ |
بیشتر بخوانید: ۱۱ روش افزایش مقاومت فشاری بتن
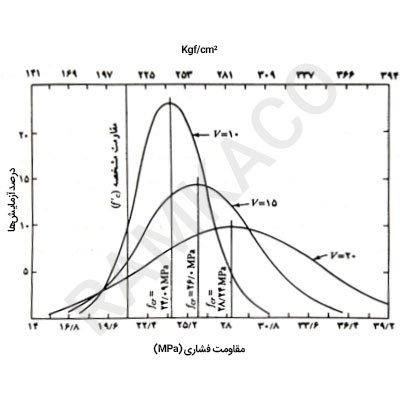
هنگام محاسبات هر آزمایش، ضریب V1 برای کنترل کارگاهی برابر ۵% فرض میشود (جدول ۳). برای نمونه نحوۀ محاسبه بند ۱ تا ۴، جدول زیر ارائه شده است .
| شماره آزمایش | نمونه استوانهای ۱ X | نمونه استوانهای ۱ X-X̅ | نمونه استوانهای ۱ ۲(X-X̅) | نمونه استوانهای ۲ X | نمونه استوانهای ۲ X-X̅ | نمونه استوانهای ۲ ۲(X-X̅) | میانگین (X) 1 و ۲ | دامنه R | میانگین متحرک مقاومت | میانگین متحرک دامنه |
| ۱ | ۲۳٫۱ | ۱٫۲ | ۱٫۴۴ | ۲۱٫۷ | ۲٫۶ | ۶٫۷۶ | ۲۲٫۴ | ۱٫۴ | ||
| 2 | 25.9 | 1.6 | 2.56 | 26.6 | 2.3 | 5.29 | 26.3 | 0.7 | ||
| 3 | 22.4 | 1.9 | 3.61 | 23.1 | 1.2 | 1.44 | 22.8 | 0.7 | ||
| 4 | 25.2 | 0.9 | 0.81 | 23.8 | 0.5 | 0.25 | 24.5 | 1.4 | ||
| 5 | 22.4 | 1.9 | 3.61 | 21 | 3.3 | 10.89 | 21.7 | 1.4 | 23.54 | |
| 6 | 26.6 | 2.3 | 5.29 | 24.5 | 0.2 | 0.04 | 25.6 | 2.1 | 24.18 | |
| 7 | 28 | 3.7 | 13.69 | 26.6 | 2.3 | 5.29 | 27.3 | 1.4 | 24.38 | |
| 8 | 23.1 | 1.2 | 1.44 | 25.2 | 0.9 | 0.81 | 24.2 | 2.1 | 24.66 | |
| 9 | 22.4 | 1.9 | 3.61 | 21 | 3.3 | 10.89 | 21.7 | 1.4 | 24.1 | |
| 10 | 21 | 3.3 | 10.89 | 22.4 | 1.9 | 3.61 | 21.7 | 1.4 | 24.1 | 1.4 |
| 11 | 21 | 3.3 | 10.89 | 21.7 | 2.6 | 6.76 | 21.4 | 0.7 | 23.26 | 1.33 |
| 12 | 22.4 | 1.9 | 3.61 | 23.1 | 1.2 | 1.44 | 22.8 | 0.7 | 22.36 | 1.33 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 30 | 23.8 | 0.5 | 0.25 | 24.5 | 0.2 | 0.04 | 24.2 | 0.7 | 22.96 | 1.05 |
| 724.5 | 175.5 | 732.9 | 262.7 | 37.8 |
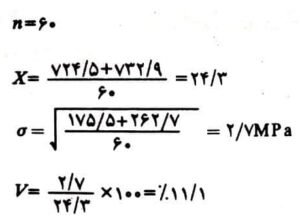
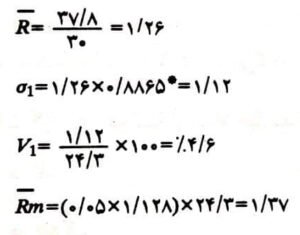
*ضریب از جدول ۲ به دست آمده است.
منحنی فراوانی- توزیع مقاومت بتن
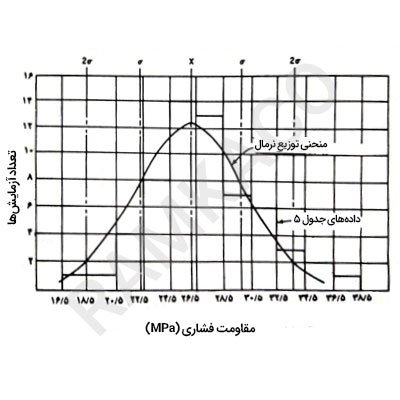
گاهی اوقات در تحلیل نتایج مقاومت بتن و هنگام ارزیابی آماری یک پروژه معین، لازم است انحراف دادهها تعیین شود. این مسأله با رسم هیستوگرام دادهها حل میشود. اگر منحنی حاصل از منحنی توزیع نرمال پیروی نکند، برخی عوامل مؤثر وجود دارند که نیازمند مطالعات گستردهتری هستند. این هیستوگرام با چیدن تمام نتایج مقاومتها در دستهها یا ناحیهها رسم میشود. منظور از ناحیه در این قسمت، ناحیه بین حداکثر و حداقل مقاومت داده شده است و هر آزمایش بین این دو عدد در آن ناحیه قرار میگیرد. در نظر داشته باشید حداقل بایستی ۱۰ ناحیه وجود داشته باشد.
حدود ناحیههای انتخابی باید به گونهای باشد که هر آزمایش مشخصاً در یک ناحیه خاص قرار گیرد. بنابراین مقاومتهای فشاری به نزدیکترین ۱ مگاپاسکال گرد میشوند. اگر حدود انتهایی ناحیهها به ۰٫۵ ختم شوند، نظیر ۱۶٫۵ – ۱۸٫۵ – ۲۰٫۵ و ….. یا با تعیین یک حد انتهایی برابر صفر و دیگری به ۰٫۹ ختم شود، نظیر ۱۸٫۹ – ۱۸ و ۱۷٫۹ – ۱۷، این امر به آسانی محقق میگردد. جدول زیر روش مناسبی برای دستهبندی را نشان میدهد.
| حدود ناحیه | تعداد نتایج آزمایش واقع در ناحیه | تعداد کل |
| ۱۶٫۵ | ||
| 18.5 | / | 1 |
| 20.5 | / | 1 |
| 22.5 | //// | 4 |
| 24.5 | /// | 8 |
| 26.5 | //// | 14 |
| 28.5 | /// | 13 |
| 30.5 | // | 7 |
| 32.5 | / | 6 |
| 34.5 | /// | 3 |
| 36.5 | // | 2 |
| 38.5 | / | 1 |
| مجموع | ۶۰ |
منحنی نرمال با محاسبه ارتفاع نقاط درX̅، X̅±σ و X̅±۲σ و سپس رسم منحنی هموار بین این نقاط و با توجه به نقاط عطف X̅±σ ترسیم میگردد که در شکل زیر نشان داده شده است.
معادلات لازم برای محاسبۀ این نقاط عبارتند از:
در y=0.3989nc/σ ،X̅
در y=0.242nc/σ ،X̅±σ
در y=0.054nc/σ ،X̅±۲σ
که در این معادلات:
X̅: مقاومت متوسط
n: تعداد کل نمونهها
σ: انحراف معیار
c: دامنۀ مقاومت یا اندازه هر ناحیه
اهمیت تحلیل آماری مقاومت بتن
آییننامه ساختمانی ACI، مفهوم آماری طبقهبندی را به شرح زیر استفاده میکند. این روش بر پایۀ به حداقل رساندن فراوانی آزمایشهای مقاومت پایینتر از مقاومت مشخصه (f’c) است. اگر تعداد این آزمایشها از این عدد محدودکننده بیشتر نشود، بتن پذیرفته میشود. برای تحقق این امر، مقاومت متوسط لازم (fcr) حتماً باید بیشتر از f’c باشد. مقداری که مقاومت متوسط لازم (fcr) باید بیشتر از مقاومت مشخصه (f’c) باشد، طی مراحلی که در روش پیشنهادی نحوه ارزیابی نتایج آزمایش مقاومت بتن (گزارش کمیته ۲۱۴ ACI) مختصراً تشریح شده، محاسبه میشود. نتایج آزمایشها بایستی با هر سه معیار زیر مطابقت داشته باشد (با توجه به حداکثر انحراف معیار و احتمال بیان شده در هر حالت):
- احتمال اینکه نتیجه هر نمونه اتفاقی مقاومت، پایینتر از مقاومت مشخصه (f’c) باشد، کمتر از ۱ در ۱۰ باشد.
- احتمال اینکه متوسط سه نمونۀ آزمایشی متوالی مقاومت، پایینتر از مقاومت مشخصه (f’c) باشد، ۱ در ۱۰۰ باشد.
- احتمال اینکه هر نمونه آزمایش، بیش از ۳٫۵ مگاپاسکال، پایینتر از مقاومت مشخصه (f’c) باشد، ۱ در ۱۰۰ باشد.
با استفاده از مقادیر t در جدول ۱، فرمولهای محاسبه مقاومت متوسط لازم برای هر یک از سه معیار بالا به این صورت خلاصه میشوند:
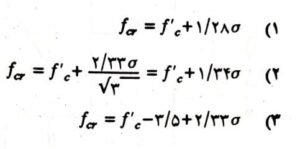
که در این روابط :
fcr : مقاومت متوسط که به عنوان اساس انتخاب نسبتهای اختلاط بتن مورد استفاده قرار میگیرد (MPa)
f’c: سطح مقاومت که در طراحی سازه مورد استفاده قرار میگیرد (مقاومت مشخصه، MPa)
σ: انحراف معیار نمونههای آزمایش مقاومت (MPa)
اگر لازم باشد مقادیر احتمال دیگری به جز مقادیری که در مشخصات ACIارائه شده است مورد استفاده قرار گیرد، مقادیر t به کار رفته در فرمولهای فوق با استفاده از جدول ۱ جایگزین میشود.
معیار ۲ همیشه موجب مقاومت متوسط لازم بالاتری نسبت به معیار ۱ میشود. در مواردی که انحراف معیار کم یا متوسط است، معیار ۲ موجب مقاومت متوسط بالاتری نسبت به معیار ۳ میشود. لیکن اگر انحراف معیار زیاد باشد، معیار ۳ حاکم است، یعنی فراوانی مورد انتظار آزمایشهایی که پیش از ۳٫۵ مگاپاسکال پایینتر از مقاومت مشخصه (f’c) هستند را به ۱ در ۱۰۰ محدود میکند.
بیشتر بخوانید: رابطه انواع مقاومت بتن
هنگامی که در یک پروژه خاص، دادههای کافی (معمولاً ۳۰ آزمایش متوالی یا بیشتر از یک رده معین بتن) وجود داشته باشد، با استفاده از این معیارها میتوان طرح اختلاط را تغییر داد. به عنوان نمونه فرض کنید در یک پروژه معین، مقاومت طراحی ۳۵مگاپاسکال به ۴۳٫۴ مگاپاسکال افزایش داده شده است. نتیجه آزمایش نمونههای مقاومت که طبق استاندارد ساخته شدهاند، نشان میدهد انحراف معیار این مخلوط ۳٫۵ مگاپاسکال است. طبق قوانین احتمال که قبلاً بیان شد، مخلوط باید از روی منحنی نسبت آب به سیمان تنظیم شود تا منجر به حصول سطح مقاومت زیر شود:
- معیار ۱:
fcr=1.28σ+ f’c
(۳٫۵×۱٫۲۸)+۳۵=fcr
۳۹٫۵=fcr
- معیار ۲:
fcr=f’c+(2.33/√۳)σ
(۳٫۵×۱٫۳۴)+f’c= fcr
۳۹٫۷=fcr
- معیار ۳:
fcr=σ۲٫۳۳+۳٫۵- f’c
(۳٫۵×۲٫۳۳)+۳٫۵-۳۵=fcr
۳۹٫۶۶=fcr
لذا ۳۹٫۷=fcr حاکم است. این مقاومت موجب استفاده از منحنی نسبت آب به سیمان برای دستیابی به مقاومت ۳۹٫۷ به جای ۴۳٫۴ میشود. لذا نسبت آب به سیمان بهبود مییابد و مخلوطی اقتصادیتر که به متعادل شدن پروژه کمک میکند، حاصل میگردد.
ملزومات طرح اختلاط بتن
آییننامه ساختمانی ACI بر استفاده از تحلیل آماری برای تعیین مقاومت مورد نیازی که ما را از حصول سطح مقاومت طراحی f’c مطمئن سازد، تأکید میکند. اگر انحراف معیار عملی بتن پروژه مشخص باشد، مقاومت متوسط لازم به دست میآید. اگر این انحراف معیار نامعلوم باشد، نسبتهای اختلاط باید به نحوی انتخاب گردند که موجب ۸٫۴ MPa مقاومت بیشتر از f’c شوند. آییننامه ساختمانی ACI، حداکثر مقادیر نسبتهای آب به سیمان در شرایط محیطی مختلف را نیز ارائه میدهد.
در این مقاله تلاش شد اصطلاحات به کار رفته در تحلیل نتایج مقاومت بتن به طور کامل تبیین شود و در کنار آن، روشهای تحلیل دادههای آماری مقاومت بتن مورد ارزیابی قرار گیرد. امیدواریم به کمک این مقاله بتوانید مقاومت بتن ساخته شده را به خوبی ارزیابی کنید.





































دست مریزاد🌹🌹
از حمایت شما متشکریم🌷
کنترل کیفیت بتن چطور انجام میشه؟
کنترل کیفیت بتن به سه دسته تقسیم میشود:
۱٫ کنترل کیفیت مصالح ورودی
۲٫ کنترل کیفیت پروسهی تولید
۳٫ کنترل کیفیت محصول نهایی که همان بتن است.
رجوع شود به استاندارد ۶۰۴۴
ممنونم از آموزش های تخصصی و حرفه ای که در اختیار مردم میگذارید.🌹
سپاس از مهر و همراهی شما.